8퀸 문제
여기서 말하는 퀸은 체스 말 중 하나인 Queen입니다.
퀸은 체스판에서 가로, 세로, 대각선으로 움직일 수 있는데
8퀸 문제는 8개의 퀸이 서로 공격했을 때, 잡을 수 없게 배치하는 문제입니다.
8퀸 문제도 하노이 탑과 마찬가지로 경우를 나누어 생각해보겠습니다.
1. 열에서 겹치지 않게, 2. 행에서 겹치지 않게, 3. 대각선으로 겹치지 않게입니다.
1. 열에서 겹치지 않게
pos = [0] * 8 # 각 열에서 퀸의 위치를 출력, pos[index] = x 일 때, index는 현재 열, x는 행
def put() -> None:
# 각 열에 배치한 퀸의 위치를 출력
for i in range(8):
print(f'{pos[i]:2}', end='')
print()
def set(i: int) -> None:
# i열에 퀸을 배치
for j in range(8):
pos[i] = j # 퀸을 j행에 배치
if i == 7:
put() # 모든 열에 퀸 배치를 끝내고 출력
else:
set(i + 1) # 다음 열에 퀸 배치
set(0) # 0 열에 퀸을 배치 시작
pos는 각 열에서 퀸의 위치를 출력합니다.
pos[0] = 0이면 퀸이 0열 0행에 있는 것이고, pos[1] = 3이면 퀸이 1열 3행에 있는 것입니다.
| 퀸 | |||||||
| 퀸 | |||||||
8x8 체스판에 위와 같이 존재하게 됩니다.
set 함수는 한 열에 하나를 놓을 때마다 set 함수를 다시 호출 해서 다음 열에 놓는다고 생각하시면 됩니다.
pos[0] = 0에서 시작 했다고 가정했을 때,
i == 7이 되면 모든 열(총 8개)에 다 놓은 것이기 때문에 출력을 해주고
다시 pos[0] = 1일 때 부터 시작합니다.
2. 행에서도 겹치지 않게
pos = [0] * 8 # 각 열에서 퀸의 위치를 출력, pos[index] = x 일 때, index는 현재 열, x는 행
flag = [False] * 8 # 각 행에 퀸을 배치했는지 체크
def put() -> None:
# 각 열에 배치한 퀸의 위치를 출력
for i in range(8):
print(f'{pos[i]:2}', end='')
print()
def set(i: int) -> None:
# i열에 퀸을 배치
for j in range(8):
if not flag[j]:
pos[i] = j # 퀸을 j행에 배치
if i == 7:
put() # 모든 열에 퀸 배치를 끝내고 출력
else:
flag[j] = True
set(i + 1) # 다음 열에 퀸 배치
flag[j] = False
set(0) # 0 열에 퀸을 배치 시작
이제 행에서도 겹치지 않게 조건을 추가했습니다.
먼저 flag 리스트는 행을 체크하기 위한 리스트입니다.
set함수를 보면 flag를 보는 조건식이 추가됐습니다.
일단 flag[j]값이 False면 not flag[j]는 True가 되고 조건식이 실행됩니다.
그럼 pos[i] = j로 퀸을 배치합니다.
퀸을 배치했다면 flag[j]에는 퀸이 있으므로 True로 바꿔주고
set(i+1)를 실행해 다른 열에도 퀸을 배치해줍니다.
set(i+1)이 끝나면 flag[j]에서 퀸을 없애야하기 때문에 false로 바꿔줍니다.
3. 대각선에서도 겹치지 않게
# 열, 행, 대각선 경우 다 포함
pos = [0] * 8 # 각 열에서 퀸의 위치를 출력, pos[index] = x 일 때, index는 현재 열, x는 행
flag = [False] * 8 # 각 행에 퀸을 배치했는지 체크
flag_a = [False] * 15 # ↗ 대각선 방향 체크
flag_b = [False] * 15 # ↖ 대각선 방향 체크
def put() -> None:
# 각 열에 배치한 퀸의 위치를 출력
for i in range(8):
for j in range(8):
print('■' if pos[i] == j else '□', end='')
print()
print()
def set(i: int) -> None:
# i열에 퀸을 배치
for j in range(8):
if ( not flag[j] # j행에 퀸이 없을 때
and not flag_a[i+j] # 대각선 방향으로 퀸이 없을 때
and not flag_b[i-j+7]): # 대각선 방향으로 퀸이 없을 때
pos[i] = j # 퀸을 j행에 배치
if i == 7:
put() # 모든 열에 퀸 배치를 끝내고 출력
else:
flag[j] = flag_a[i+j] = flag_b[i-j+7] = True
set(i + 1) # 다음 열에 퀸 배치
flag[j] = flag_a[i+j] = flag_b[i-j+7] = False
set(0) # 0 열에 퀸을 배치 시작
flag_a와 flag_b는 대각선을 따지는 리스트입니다.
리스트의 길이를 15로 한것은 8x8일 때 대각선 줄의 총 개수이기 때문입니다.
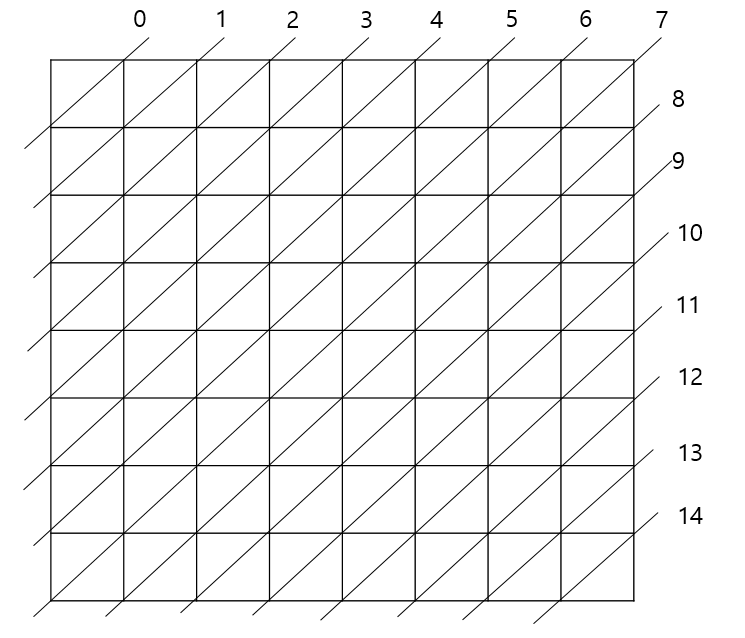
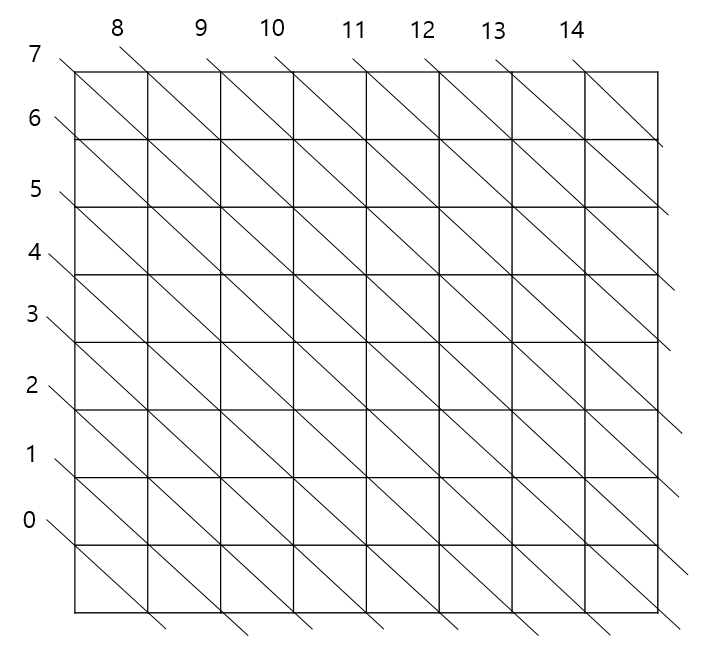
이런 식으로 총 15개입니다.
그래서 flag_a, flag_b의 인덱스는 저기있는 숫자라고 생각하시면 됩니다.
i와 j가 0, 0이면 flag_a[0], flag_b[7] 라인에서 겹치는게 있는지 검사하면 되는 겁니다.
put 함수는 처음 말했듯이 pos[i] = j에 퀸을 놓는 것이기 때문에
pos[i] = j일 경우에는 검은 네모를, 아닐 경우에는 빈 네모를 출력합니다.
결과

이런 식으로 결과가 출력되고, 다 출력이 된다면 92개가 출력됩니다.
'IT > 알고리즘' 카테고리의 다른 글
| 알고리즘 - 버블 정렬 (0) | 2020.11.20 |
|---|---|
| 백준 - 6603번 (0) | 2020.11.19 |
| 백준 - 17478번 (0) | 2020.11.18 |
| 백준 - 1914번 (0) | 2020.11.18 |
| 알고리즘 - 재귀 알고리즘(2) (0) | 2020.11.18 |


댓글