단순 삽입 정렬의 장점은 살리고 단점을 보완해, 더 빠르게 정렬하는 알고리즘을 셸 정렬이라고 합니다.
셸 정렬은 먼저 정렬할 배열의 원소를 그룹으로 나누어, 각 그룹별로 정렬을 수행합니다.
그리고 정렬된 그룹을 합치는 작업을 반복하여 원소의 이동 횟수를 줄이는 방법입니다.

위와 같이 8개의 원소를 갖는 배열이 있을 때,
단순 삽입 정렬은 1을 맨 앞으로 이동시킬 때 총 7번 이동시켜야 합니다.
셸 정렬을 하면 먼저 서로 4칸씩 떨어진 원소를 꺼내어 4개의 그룹으로 나누고 그룹별로 각각 정렬합니다.

(8, 5), (4, 2), (9, 7), (6, 1) --> (5, 8), (2, 4), (7,9), (1, 6)

이렇게 4칸 떨어진 원소를 정렬하는 방법을 4-정렬이라고 합니다.
이어서 2칸 떨어진 원소를 정렬합니다.

(5, 7, 8, 9), (2, 1, 4, 6) --> (5, 7, 8, 9), (1, 2, 4, 6) >>>>>>> 2-정렬

마지막으로 1칸 떨어진 배열을 정리해주는데 배열 전체를 정리한다고 생각하시면 됩니다.

셸 정렬을 사용하게 되면 정렬 횟수는 늘어나지만
전체적으로 원소의 이동 횟수가 줄어들어 효율적이게 됩니다.
def shell_sort(a):
n = len(a)
h = n // 2 # 4-정렬, 2-정렬 >> h-정렬
while h > 0:
for i in range(h, n):
j = i - h
print(f'그룹 인덱스: {j}, {i}')
tmp = a[i]
while j >= 0 and a[j] > tmp:
a[j+h] = a[j]
j -= h
a[j+h] = tmp
print(f'정렬 결과 {a}')
h = h // 2
print()
print('셸 정렬')
num = int(input('원소 소 입력: '))
x = [None] * num
for i in range(num):
x[i] = int(input(f'x[{i}]: '))
shell_sort(x)
h는 위에서 언급한 4-정렬, 2-정렬에서 숫자라고 생각하시면 됩니다.
h는 전체 길이의 반으로 시작합니다.
첫 번째 while문에서 for문의 범위는 h~n까지인데
배열의 길이가 8이라고 가정하면 4~8이고 h-정렬에서 정렬을 진행하는 횟수의 범위와 같습니다.
tmp는 교환을 진행할 원소입니다.
두 번째 while문은 교환을 진행하는 반복문입니다.
반복문이 끝나면 h를 다시 반으로 나누어 주고 다음 h-정렬을 시작합니다.
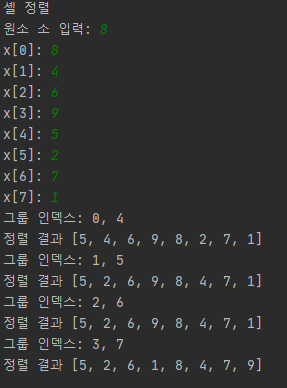
먼저 4-정렬 결과창입니다.
(0, 4), (1, 5), (2, 6), (3, 7)로 나뉘어 정렬을 하는 것을 볼 수 있습니다.

다음은 2-정렬 입니다.
(0, 2) -> (2, 4) -> (4, 6) // (1, 3) -> (3, 5) -> (5, 7)
두 그룹으로 나누어 정렬 하는 것을 볼 수 있습니다.

마지막으로 1-정렬(전체 정렬)로
최종적으로 오름차순으로 완벽하게 정렬되는 것을 확인할 수 있습니다.

위 배열에서 4-정렬과, 2-정렬을 해봅시다.


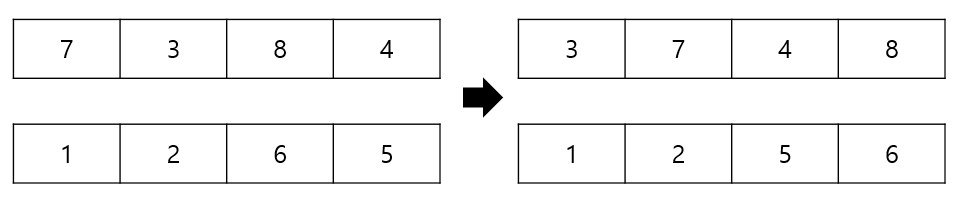

원래 배열과 2-정렬까지 끝낸 배열을 보면 정렬을 했음에도 원래 배열과 크게 다를게 없습니다.
그룹을 나누어 진행했음에도 충분히 기능을 하지 못하고 있습니다.
이 문제를 해결하기 위해서는 h값이 서로 배수가 되지 않도록 해야하고
그래야 효율 좋은 정렬을 기대할 수 있습니다.
def shell_sort(a):
n = len(a)
h = 1
while h < n // 9:
h = h * 3 + 1
while h > 0:
for i in range(h, n):
j = i - h
tmp = a[i]
print(f'그룹 인덱스: {j}, {h}')
while j >= 0 and a[j] > tmp:
a[j+h] = a[j]
j -= h
a[j+h] = tmp
print(f'정렬 결과 {a}')
h = h // 3
print('셸 정렬')
num = int(input('원소 소 입력: '))
x = [None] * num
for i in range(num):
x[i] = int(input(f'x[{i}]: '))
shell_sort(x)
기존 셸 정렬과 차이점은 h가 1로 시작하고
h값을 h * 3 + 1로 하여 배수가 되는 것을 피한 것입니다.

셸 정렬의 시간 복잡도는 단순 정렬보다 매우 빠르지만, 셸 정렬은 이웃하지 않고 떨어져 있는 원소를 서로 교환하기 때문에 안정적이지 않은 문제가 있습니다.
'IT > 알고리즘' 카테고리의 다른 글
| 백준 - 10610번 (0) | 2020.11.25 |
|---|---|
| 백준 - 10815번 (0) | 2020.11.24 |
| 알고리즘 - 이진 삽입 정렬 (0) | 2020.11.23 |
| 알고리즘 - 단순 삽입 정렬 (0) | 2020.11.23 |
| 알고리즘 - 버블 정렬 (0) | 2020.11.20 |


댓글